Logistic regression model

This page shows the addition of a logistic regression formula on Evidencio. The standard formula for a logistic regression is: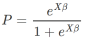
β₀ is the intercept and Xβ is the model linear predictor. Estimated by the summation of the intercept term and all β values multiplied by that variable. E.g.: β₀ + β_var1 ⋅ var1 + β_var2 ⋅ var2.

Numerous logistic regression based models can be found in published research. However, not all models describe the coeficients necessary to add a model on Evidencio. Most models do show the results of the multivariate analysis as odds ratios. The beta coefficients can be calculated by taking the natural logarithm of the odds ratio. Besides, on Evidencio it is possible to enter odds ratios instead of beta coefficients. The intercept, however, is really necessary to add the model on Evidencio. Without the intercept, the calculations will be faulty.

A step-by-step guide to add a logistic regression model is seen below. A novel Briganti model is the example used in this case, described by Gandaglia et al. (2017). Original article can be found here.
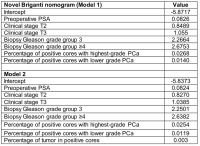
The coefficients used in this model were added as supplementary data, the model added in this guide concerns model 1, found in the table below.

• Go to www.evidencio.com, make sure that you're signed in, click on Models and on New Model in the drop-down menu. Make sure to fill all the fields up-to the fourth sub-tab Model. More information on how to fill in the rest of the model can be found over here.
• Select Logistic regression, Beta coefficients, Single value, and enter the Intercept (-5.8717) and the C-statistic(0.908). (Example)
• Add the variables that can be found on the table above. Make sure to check in the description of the model developers what the ranges, units and reference values are for the variables. Also make sure if any conversions are needed in the model.(Example)
• If your input matches the description of the model development, your model is now ready to be used. Make sure that the Pre-Result text is filled in, so users know what they predict. Always try out your model before setting it to public to make sure that it works properly. (Example of a calculation)

The example above shows a model where all the coefficients were given. This is of course very nice, but is unfortunately not always described very well. Several models display the odds ratios and a nomogram, but the intercept is missing. The example above of the Novel Briganti model also used a nomogram in their published work. The nomogram is displayed below:

So what if we only have the odds ratios and this nomogram for this model. We can actually derive the intercept based on the input in a nomogram.

• We know the beta coefficients if we have the odds ratios. In the nomogram above we can see that PSA is a predictor where the PSA level of 50 ng/ml gets 100 points assigned. So the increase of 1 ng/ml PSA adds 2 points to the calculation.
• We know that the beta coefficient of PSA is 0.0826 (odds ratio 1.086). So every point in the nomogram is worth 0.0413 beta.(0.0826/2)
• We can see in the nomogram that 80 points corresponds with a risk of 7% and a risk of 60% corresponds with approximately 152 points.
  • ∑βX for 80 points is equal to 80 · 0.0413 = 3.304.
  • ∑βX for 152 points is equal to 150 · 0.0413 = 6.195.
• Now we have all the parts of the equation except for the intercept for two different examples. We can enter the formula without the intercept and solve the equation.
  • For the 80 points = 7% risk example we get an intercept of -5.89069
  • For the 152 points = 60% risk example we get an intercept of -5.78953
  • On average our intercept is -5.84011.
  • The intercept of the example model is given, so if we compare our derivation with the given intercept we see that the intercept should be -5.8717.
• With this derivation we can estimate the intercept, but bear in mind that this estimation might not be completely accurate! Still using the formula instead of the nomogram improves accuracy measures and makes it more efficient to calculate a risk.